Орбитальные элементы спутника

Для определения орбиты и положения космического аппарата вдоль нее используются шесть величин, называемых кеплеровскими величинами. Первые два – это тип и размер орбиты (определяемые эксцентриситетом и большой полуосью); еще три (наклон, долгота восходящего узла и аргумент периапсиса) определяют ориентацию орбиты относительно инерциальной системы отсчета; и последнее – это положение тела вдоль орбиты (истинная аномалия).

Для эллиптической орбиты вокруг небесного тела точка на орбите, которая находится ближе всего к орбитальному небесному телу, называется периапсисом (P), а самая дальняя точка – апоапсисом (A). Прямая линия, соединяющая периапсис и апоапсис, является линией апсид. Это главная ось эллипса, его наибольший диаметр. Центр масс (или барицентр) системы из двух тел находится на этой линии в одном из двух фокусов эллипса.

Свойства Орбит спутника 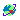можно задать в Инженерной базе данных:

Эксцентриситет (e) – это параметр, который определяет величину отклонения орбиты спутника вокруг небесного тела от идеального круга. Значение 0 представляет собой круговую орбиту, значения от 0 до 1 образуют эллиптическую орбиту, 1 – параболическую орбиту освобождения, а больше 1 – гиперболу. Эксцентриситет эллипса определяется как e = f/a, где f – расстояние от центра до одного из фокусов.
Большая полуось (а) составляет половину расстояния от апоапса до периапсиса.
Наклон (i) – это угол между плоскостью орбиты и базовой плоскостью, в которой находится барицентр. Экваториальная плоскость является базовой плоскостью для спутниковых орбит, а эклиптика (плоскость орбиты вокруг Солнца) – для небесных тел (планет и спутников).
Долгота восходящего узла () – это угол от базового направления, называемого началом долготы, к направлению восходящего узла, измеренный в базовой плоскости. Для орбит спутника началом долготы является Весеннее равноденствие (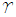). Восходящий узел (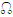) – это точка, в которой орбитальный объект движется на север через базовую плоскость, а нисходящий узел находится там, где он движется на юг через эту плоскость.
Вращение орбиты в плоскости орбиты измеряется с помощью параметра Аргумент периапсиса (ω), это угол в базовой плоскости, взятый от начала долготы до восходящего узла орбиты (в направлении против часовой стрелки или в восточном направлении).
Положение спутника на орбите определяется истинной аномалией (ν), которая определяет положение орбитального тела вдоль эллипса в определенный момент времени («в эпоху»). Это угол между направлением периапсиса и текущим положением спутника, если смотреть от барицентра. Средняя аномалия – это угловое расстояние от периапсиса, которое было бы у условного тела, если бы оно двигалось по круговой орбите с постоянной скоростью в том же орбитальном периоде, что и фактическое тело на его эллиптической орбите. Это математически удобный "угол", который изменяется линейно со временем, но не соответствует реальному геометрическому углу и может быть преобразован в истинную аномалию.

Рис. 1. Орбитальные элементы.

После выбора объекта Орбита спутника следует задать его ориентацию в диалоговом окне Мастер проекта или Общие настройки.

Существует два типа ориентации, которую можно задать для космического аппарата:

Выравнивание и ограничение. Оси фиксированного тела ориентируются с использованием выровненных и ограниченных пар векторов. В первой паре вектор фиксированного тела (Выровненный вектор), определенный с использованием выбранной оси Глобальной системы координат по умолчанию, выравнивается с заданным базовым вектором. Во второй паре другой вектор фиксированного тела (Ограниченный вектор), также определенный с помощью выбранной оси Глобальной системы координат по умолчанию, ограничивается в направлении другого базового вектора.

Существуют следующие базовые векторы:
- Направление надира. Вектор фиксированного тела выровнен с направлением надира, указывающим на центр планеты.
- Вектор скорости. Вектор фиксированного тела совпадает с направлением скорости космического аппарата.
- В направлении весеннего равноденствия. Вектор фиксированного тела совпадает с направлением весеннего равноденствия. Весеннее равноденствие – одна из двух точек в небесной сфере, где эклиптика и небесный экватор пересекаются, когда Солнце пересекает небесный экватор, идущий на север.
- К Солнцу. Вектор фиксированного тела совпадает с направлением Солнца.

Выравнивание спинов описывает вращение вокруг заданного Выровненного вектора с постоянной Угловой скоростью.

Исходная ориентация космического аппарата задается с использованием Начального угла поворота, измеряемого от Ограниченного вектора в плоскости, перпендикулярной оси вращения.

Оси фиксированного тела ориентируются с использованием выровненных и ограниченных пар векторов, аналогично типу ориентации Выровнено и ограничено.