Параметры визуализации вихревых структур

Для большинства задач гидромеханики характерно наличие вихревых структур. Несмотря на то, что по сути идея вихря имеет фундаментальное значение для механики жидкости, до сих пор нет единого мнения относительно общепринятого и строгого определения этого явления явного потока. По одному из определений вихревое движение представляет собой вращательное движение множества материальных частиц вокруг общего центра. Критериями существования вихря являются замкнутые или спиральные линии тока, локальный минимум давления, а также изолинии и изоповерхности завихренности. Однако эти критерии имеют свои недостатки. Так, чтобы определить наличие вихря с помощью спиральных линий тока, необходимо выполнить их исследование. Существование локального минимума давления не может гарантировать наличие вихря (и наоборот). В настоящее время нет ответа на вопрос, какой идентификатор вихрей является наиболее точным в общем случае.

Завихренность

Для идентификации вихря достаточно часто используется тензор завихренности (dGu), который определяется как инвариантная (т. е. не зависящая от скорости поступательного движения наблюдателя) галилеева величина, выражающая среднюю угловую скорость элементов текучей среды.

Завихренность рассчитывается следующим образом:

в абсолютной (т. е. неподвижной) системе координат этот параметр определятся как вектор 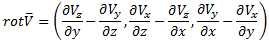и/или его модуль, где V – вектор скорости потока;
в системе координат, вращающейся с угловой скоростью ω, этот параметр определятся как вектор 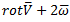и/или его модуль (здесь V – вектор скорости потока в той же системе координат).

Завихренность характеризует вращение твердой частицы P' вокруг соседней твердой частицы P. Таким образом, скорость вращения в абсолютной (т. е. неподвижной) системе координат равна 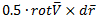, где 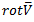– завихренность в точке P, 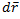– расстояние от точки P до точки P'.

Тем не менее, в идентификации вихря завихренность играет свою роль менее очевидно, чем ожидается. Однако для определения существования вихря наиболее широко применяются локальные методы, основанные на исследовании тензора градиентов скорости 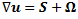, его симметричной и асимметричной частей, тензора скоростей деформаций S и тензора завихренности W, соответственно, и трех инвариант du, где 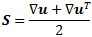и .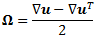

Критерий Lambda2

Критерий λ2 (Jeong, J. & Hussain, F. 1995. On the identification of a vortex. J. Fluid Mech. 285, 69–94 .) вводится на основании следующего наблюдения: в задачах, в которых преобладают вязкие силы и нестационарные напряжения, принцип локального минимума давления является недостаточным для выявления вихревой структуры. Если пренебречь вязким и нестационарным слагаемыми, то симметричная часть градиента уравнения Навье-Стокса для несжимаемой жидкости может быть выражена следующим образом:

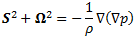
Информация о локальном экстремуме давления содержится в гессиане давления (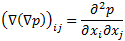). Для возникновения локального минимума давления в плоскости поперек вихря требуется, чтобы гессиан давления имела два положительных собственных числа. Вихрь рассматривается как область текучей среды с двумя отрицательными собственными числами тензора S2 + W2. Т.к. тензор S2+W2 является симметричным, то существует только три действительных собственных числа. Если упорядочить их следующим образом – λ1 ≥ λ2 ≥ λ3, то критерий идентификации вихря будет эквивалентен результирующему условию λ2 < 0.