Графики FFT
На практике, чтобы записать сигнал в цифровом виде, его из непрерывного формата переводят в дискретный (по времени). Для преобразования дискретного сигнала (дискретного по времени) во временной области в противоположный сигнал (дискретный по частоте) в частотной области применяется Дискретное преобразование Фурье (DFT).
Прямое дискретное преобразование Фурье для перехода от временной области к частотной области:
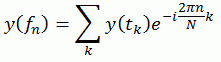 | (1) |
|---|
Обратное дискретное преобразование Фурье для перехода от частотной области к временной области:
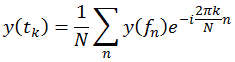 | (2) |
|---|
где N – количество экспериментальных точек во временном периоде, n – индекс частоты,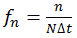 
– частота, 
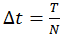– шаг по времени, T – временной период эксперимента.
При работе в реальных проектах для уменьшения времени расчета DFT часто используется алгоритм Быстрого преобразования Фурье (FFT). Этот алгоритм вычисляет преобразование Фурье в N/log(N) – 1 раз быстрее по сравнению с алгоритмом DFT.
График FFT позволяет анализировать данные давления, Нестационарность, используя алгоритм Быстрого преобразования Фурье (FFT). Доступны следующие параметры:
Спектральная плотность мощности [Па2] – распределение сигнала в частотной области:
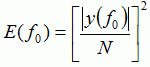
(3) 
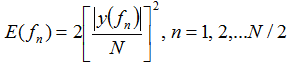
(4)
Амплитуда [Па] – амплитуда сигнала:
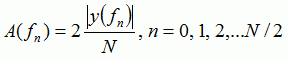
(5)
Уровень звукового давления [дБ] – уровень сигнала:
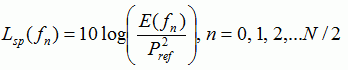
(6) где Pref – опорное звуковое давление, равное 2·10-5 Па.
Амплитуда звуковых колебаний [дБ]:
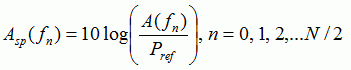
(7)
Данные экспортируются в книгу Microsoft Excel, в которой отображаются графики и значения параметров. Графики отображаются на отдельных листах, а все значения параметра выводятся на листе Данные.
Кроме экспорта данных в книгу Microsoft Excel, график можно отобразить в качестве виджета в графической области, а также в качестве графика в панели в нижней части экрана.
Другие действия, доступные при нажатии правой кнопкой мыши на элемент, описаны в разделе “Элементы дерева анализа CADFLO”.