Неньютоновские жидкости
Все доступные модели неньютоновских жидкостей основаны на предположении, что сдвиговые напряжения (τ) в такой среде являются функцией скорости сдвиговых деформаций (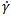 ):
):
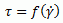 | (1) |
|---|
или используют динамическую вязкость жидкости (μ) по аналогии с ньютоновскими жидкостями.
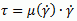 | (2) |
|---|
Пользователь может выбрать одну из пяти доступных моделей неньютоновских жидкостей:
Модель Гершеля-Балкли (Herschel-Bulkley)
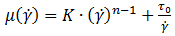
(3) где K – коэффициент консистентности (Па·сn), n – показатель степени жидкости (безразмерный), τ0 – предел текучести жидкости (Па).
Эта модель имеет следующие частные случаи:
n = 1, τ0 = 0: ньютоновские жидкости, в этом случае K – динамическая вязкость жидкости;
n = 1, τ0 > 0: неньютоновские жидкости, описываемые моделью Бингема, особенностью которых является ненулевая величина предела текучести (τ0). Ниже этого предела жидкость ведет себя как твердое тело, и для перехода в жидкое состояние она должна превзойти это пороговое сдвиговое напряжение (которое моделируется с помощью автоматического приравнивания коэффициента K, который в данном случае называется пластической вязкостью, к достаточно высокому значению при τ < τ0);
0 < n < 1, τ0 = 0: неньютоновские жидкости, описываемые степенной моделью, вязкость которых увеличивается при увеличении скорости сдвиговых деформаций;
n > 1, τ0 = 0: неньютоновские жидкости, описываемые степенной моделью, вязкость которых уменьшается при увеличении скорости сдвиговых деформаций.
Степенная модель
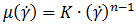
(4) в отличии от указанного выше случая для модели Гершеля‑Балкли в данном случае значения μ ограничены: μmin ≤ μ ≤ μmax, поэтому эти значения минимальной и максимальной вязкости в Па·с задаются в дополнение к коэффиценту консистентности (K), в Па·сn, в показателю степени (n), (безразмерный).
Модель Каро (Carreau)
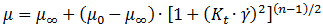
(5) здесь:
μ∞ – динамическая вязкость жидкости при бесконечно большой скорости сдвиговой деформации, т. е. минимальная динамическая вязкость (Па·с);
μ0 – динамическая вязкость жидкости при нулевой скорости сдвиговой деформации, т. е. максимальная динамическая вязкость (Па·с);
Kt – постоянная времени (с);
n – показатель степени (безразмерный).
Эта модель – вариант сглаживания степенной модели с ограничениями на величину μ.
Все параметры описанных выше моделей, за исключением безразмерного показателя степени n , могут быть заданы зависящими от температуры.
Модель Кросса-Вильямса-Ландела-Ферри (Cross-WLF (Cross-William-Landel-Ferry)
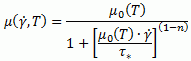
(6) здесь:
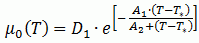 – динамическая вязкость при нулевой скорости сдвиговой деформации или «ньютоновский предел», при котором вязкость стремится к постоянному значению при очень низких скоростях сдвиговых деформаций;
– динамическая вязкость при нулевой скорости сдвиговой деформации или «ньютоновский предел», при котором вязкость стремится к постоянному значению при очень низких скоростях сдвиговых деформаций;T* = D2 – температура стеклования (K);
n – показатель степени в режиме высокой скорости сдвиговой деформации (безразмерный, 0 < n ≤ 1);
τ* – уровень критического напряжения при переходе к псевдопластичности;
A1 (безразмерный), A2(K),D1 (Па·с) и D2 (K) – константы, соответствующие данным.
Эта модель является другим вариантом степенной модели для псевдопластических жидкостей с учетом влияния температуры (T).
Модель второго порядка
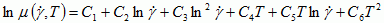
(7) где Ci, i = 1...6 – коэффициенты, которые задаются пользователем.
Шесть коэффициентов Ci могут быть определены путем задания двух наборов значений вязкости (
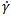 i, μi) при температурах T1 и T2 соответственно и выполнения одновременной мультирегрессионной минимизации методом наименьших квадратов. Таким образом, это уравнение описывает основную кривую вязкости в узком диапазоне рабочих температур между нижней границей (T1) и верхней границей (T2). За пределами этого диапазона или в случае, если этот диапазон становится слишком широким, точность уравнения может постепенно снижаться.
i, μi) при температурах T1 и T2 соответственно и выполнения одновременной мультирегрессионной минимизации методом наименьших квадратов. Таким образом, это уравнение описывает основную кривую вязкости в узком диапазоне рабочих температур между нижней границей (T1) и верхней границей (T2). За пределами этого диапазона или в случае, если этот диапазон становится слишком широким, точность уравнения может постепенно снижаться.Если выбран параметр Задать минимальное значение сдвиговой скорости, можно указать Min значение скорости деформации, после которого вязкость (
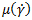 ) считается постоянной.
) считается постоянной.
Модель с таблицей вязкости
Модель с таблицей вязкости определяет значения динамической вязкости
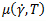 путем линейной интерполяции или полиномиальной аппроксимации табличных зависимостей вязкости (μ) (Па·с) от скорости сдвиговых деформаций (
путем линейной интерполяции или полиномиальной аппроксимации табличных зависимостей вязкости (μ) (Па·с) от скорости сдвиговых деформаций (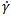 ) (с-1) при различных температурах (T) (К).
) (с-1) при различных температурах (T) (К).Чтобы задать табличные зависимости, выберите модель с таблицей вязкости при создании или изменении неньютоновской жидкости в Инженерной базе данных и перейдите на вкладку Таблицы и графики. Помимо задания таблицы вязкостей, необходимо также выбрать один из следующих Методов аппроксимации этих зависимостей:
Линейный. Выполняется линейная интерполяция значений, заданных в таблице, при этом вязкость вне табличного диапазона считается постоянной (
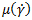 = const). Для метода линейной интерполяции таблица сопоставления значений Вязкости и Скорости деформаций должна содержать две или более строк для каждого значения Температуры.
= const). Для метода линейной интерполяции таблица сопоставления значений Вязкости и Скорости деформаций должна содержать две или более строк для каждого значения Температуры.Аппроксимация полиномом 2-го порядка. Коэффициенты полинома автоматически определяются методом наименьших квадратов. В этом случае необходимо задать по крайней мере три зависимости Вязкости от Скорости деформаций для каждого значения Температуры.
Аппроксимация полиномом 3-го порядка. Коэффициенты полинома автоматически определяются методом наименьших квадратов. В этом случае необходимо задать по крайней мере четыре зависимости Вязкости от Скорости деформаций для каждого значения Температуры.
СоветДля псевдопластических неньютоновских жидкостей характерна следующая зависимость: когда скорость сдвиговых деформаций стремится к нулю, их вязкость существенно возрастает. Поэтому при задания вязкости таких жидкостей рекомендуется использовать метод аппроксимации Полиномом 3-го порядка.
Если выбран параметр Задать максимальное значение сдвиговой скорости, можно указать Макс. значение скорости деформации, после которого
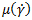 считается постоянной.
считается постоянной.
В задаче Вы можете рассматривать смесь нескольких неньютоновских жидкостей, причем они могут описываться разными моделями. Однако свойства этих жидкостей не должны сильно различаться.