Целевая функция

Задание целевой функции:-

• Режим Целевая функция позволяет задать уравнение целевой функции.

  • В режиме Планирование экспериментов и оптимизация выберите один из вариантов режима Целевая функция: Минимизировать, Максимизировать или Искомое значение:

    • Минимизировать (Максимизировать). В этом случае выполняется поиск минимума (максимума) линейной целевой функции вида:

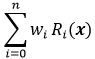
      	(1)

      где n – количество параметров отклика Ri с весовыми коэффициентами wi, x – вектор проектного параметра.

    • Искомое значение. В этом случае необходимо задать искомое значение для каждого выходного параметра. Затем будет выбран параметр x и выполнена минимизация целевой функции вида:

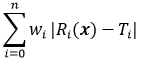
      	(2)

      где n – количество параметров отклика Ri с целевыми значениями Ti и весовыми коэффициентами wi. Цель – максимально привести все параметры отклика к искомым значениям.

    • Для каждого выходного параметра необходимо задать следующие параметры:

      • искомое значение. Нужное искомое значение Ti , соответствующее выбранной переменной решения (доступно только для типа Искомое значение).

      • весовой коэффициент. Весовой коэффициент целевой функции wi соответствует выбранной переменной решения.

  • При необходимости можно добавить и задать Ограничение на переменные решения:

    • Чтобы добавить новое ограничение, нажмите кнопку Добавить ограничение .

    • Чтобы удалить выбранное ограничение, нажмите кнопку Удалить ограничение .

    • Для каждого Ограничения задайте следующие параметры:

      • Выберите правило решения: Меньше или Больше.

      • Установите граничное Значение выходного параметра.

      • Задайте весовой коэффициент для выбранного выходного параметра.

    • В группе Выражение проверьте режим оптимизации целевой функции и заданные ограничения (в строке При условии).

    • Чтобы добавить точку оптимума в таблицу экспериментов, нажмите на кнопку Добавить оптимальную расчетную точку.

      Для получения оптимального отклика используется метод сопряженных градиентов.

      Для Оптимальной расчетной точки величину Ошибка RSM, представляющую собой выборочное стандартное отклонение различий между прогнозируемыми и фактическими значениями, можно определить как квадратный корень из среднеквадратической ошибки.