Глоссарий
Акустическая мощность
Proudman (I. Proudman. The Generation of Noise by Isotropic Turbulence. Proc. Roy. Soc., A214:119, 1952.) – выводится формула расчета мощности звуковых колебаний, генерируемых изотропным турбулентным потоком без учета среднего течения, с использованием акустической аналогии Лайтхилла. Lilley (G. M. Lilley. The radiated noise from isotropic turbulence revisited. NASA Contract Report 93-75, NASA Langley Research Center, Hampton, VA, 1993.) – повторно выводится формула с учетом разницы запаздывающего времени, которая не учитывалась в исходном выводе Прудмана. В обоих случаях Акустическая мощность (Вт/м3) для единичного объема изотропной турбулентности определяется следующим образом:
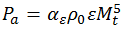
где 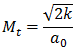 – турбулентное число Маха; αe – константа модели, равная 0.1, на основе калибровки Саркара и Хуссаини (S. Sarkar and M. Y. Hussaini. Computation of the sound generated by isotropic turbulence. NASA Contract Report 93-74, NASA Langley Research Center, Hampton, VA, 1993.); ρ – плотность среды; ε – диссипация энергии турбулентности; k – кинетическая энергия турбулентности; a0 – скорость звука.
– турбулентное число Маха; αe – константа модели, равная 0.1, на основе калибровки Саркара и Хуссаини (S. Sarkar and M. Y. Hussaini. Computation of the sound generated by isotropic turbulence. NASA Contract Report 93-74, NASA Langley Research Center, Hampton, VA, 1993.); ρ – плотность среды; ε – диссипация энергии турбулентности; k – кинетическая энергия турбулентности; a0 – скорость звука.
Суммарная акустическая мощность (W/m3) может быть также выражена в дБ как Уровень акустической мощности:
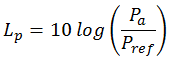
где Pref = 10–12 Вт/м3 – опорная акустическая мощность.
Реализованная модель источника широкополосного шума не требует нестационарных решений. Однако она позволяет получить только основные характеристики шума и может быть использована для диагностирования источника шума и определения той части течения, которое отвечает за создание шума.
Формула Прудмана позволяет оценить уровень локального вклада в общую акустическую мощность на единицу объема в заданном поле турбулентности. При исследовании результатов расчета следует учитывать ограничения используемого подхода: большое число Рейнольдса, малое число Маха, изотропия турбулентности и нулевое среднее движение.
Базовая сетка (глобальная сетка)
Базовая сетка строится по всей расчетной области. Расчетная область разбивается на части параллельными плоскостями, перпендикулярными осям Глобальной системы координат. Среди этих плоскостей находятся граничные плоскости расчетной области (в точке X мин,..., Z макс).
По умолчанию базовая сетка является равномерной (т. е. ее плоскости почти равноудалены друг от друга в направлениях X, Y и Z Глобальной системы координат). Расстояния между плоскостями определяются по числу заданных в этих направлениях ячеек (Nx, Ny, Nz). При необходимости можно вставлять дополнительные плоскости сеток и указывать другие интервалы между ними (т. е. расположить их неравномерно). Для этого создайте Контрольные плоскости (см. раздел “Контрольные плоскости”).
Сжимаемый
Течения считаются сжимаемыми, если плотность текучей среды существенно зависит от давления.
В CADFLO газы всегда считаются сжимаемыми, а жидкости могут быть как сжимаемыми, так и несжимаемыми. Если в проекте рассматривается течение газа со сверхзвуковой скоростью (в случае нестационарной задачи число Маха превышает 3, в случае нестационарной – больше 1), то в задаче необходимо это учитывать.
Для течения газа с большим числом Маха установите флажок Течение с большим числом Маха на вкладке Текучая среда в диалоговом окне Мастер проекта или Общие настройки.
Если рассматривается течение воздуха с очень большим числом Маха (M > 5), выберите параметр Гиперзвуковое течение, который становится доступным после выбора параметра Течение с большим числом Маха.
В задачах, в которых основной поток является дозвуковым, а сверхзвуковое течение наблюдается в относительно небольшом объеме, то течение рекомендуется рассматривать как течение с малым числом Маха. Если объем, в котором течение становится сверхзвуковым, занимает примерно половину расчетной области или больше, рекомендуется использовать опцию течения с большим число Маха.
Сопряженный теплообмен
CADFLO автоматически учитывает теплообмен в текучей среде, а также между текучей средой и стенками (конвекция). По умолчанию CADFLO не учитывает теплообмен в твердых телах (Теплопроводность), но эту функцию можно включить. Сочетание теплообмена с помощью конвекции и проводимости (сопряженный теплообмен) можно включить, если выбрать параметры Течение жидкости/газа и Теплопроводность на вкладке Тип задачи в диалоговом окне Мастер проекта или Общие настройки.
Системой координат
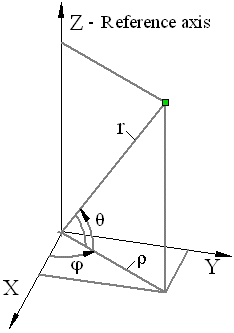
В CADFLO используются общепринятые системы координат: декартова (x, y, z), цилиндрическая (ρ, φ, z) и сферическая (r, θ, φ).
Цилиндрические координаты (ρ, φ, z) точки определяются следующим образом: осевое расстояние или радиальное расстояние (ρ), азимут (φ) и осевая координата или высота (z).
Для преобразования между цилиндрическими и декартовыми координатами удобно предположить, что цилиндрической осью является декартова ось z. Тогда координаты z одинаковы в обеих системах, и соответствие между цилиндрическими (ρ, φ, z) и декартовыми (x, y, z) координатами таково:
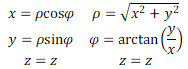
Сферические координаты (r, θ, φ) точки определяются следующим образом: радиус или радиальное расстояние (r), высота или полярный угол (θ) и азимут или угол азимута (φ). Соответствие между сферическими (r, θ, φ) и декартовыми (x, y, z) координатами таково:
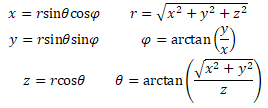
Критерия сходимости цели.
Цель сходится, если вычисленный целевой размах амплитуды (Дельта) становится меньше Критерия сходимости цели, который может определяться автоматически в CADFLO или задаваться вручную в диалоговом окне Опции управления расчетом (см. раздел “Завершение расчета”).
Значение автоматического Критерия рассчитывается следующим образом:
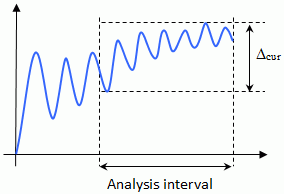
На всем интервале от итерации 3 до Продувка 1 автоматический критерий (Cr0) определяется как доля Vcr от Δcur, где Δcur – разность между максимумом и минимумом текущих значений на интервале анализа. Для большинства задач Vcr устанавливается равным 3 %, однако для модельных задач это значение может быть скорректировано (увеличено до 15 %).
Также на каждом шаге, начиная с первой продувки, рассчитывается текущий критерий (Cri). Он определяется как доля Vcr от Δcur на интервале от предыдущей продувки к текущей. Затем определяется среднее значение критерия (Crav) как среднее арифметическое всех значений Cri.
В качестве результирующего значения Критерия принимается максимальное из Crav и Cr0.
Отношение Критерия сходимости цели к действительному размаху амплитуды колебаний цели (Дельта) на всем интервале анализа называется Прогрессом сходимости цели и отображается на индикаторе сходимости (см. разделы “Таблица целей” и “Цель”).
Дельта
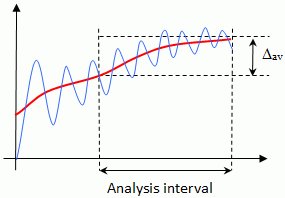
Когда CADFLO анализирует сходимость цели, вычисляется размах амплитуды колебаний цели (Дельта) как минимальное значение среди Δcur и Δav, где Δav – разница между максимальным и минимальным значениями усреднения на интервале анализа по результатам последней итерации.
|
|
Цель для значений параметра |
Цель для средних значений параметра (вычисляется как среднее арифметическое всех значений параметра) |
Цель сходится, если вычисленное значение Дельта меньше Критерия сходимости цели. сходимости цели, который может определяться автоматически в CADFLO или задаваться вручную в диалоговом окне Опции управления расчетом (см. раздел “Завершение расчета”).
Отношение Критерия сходимости цели к действительному размаху амплитуды колебаний цели (Дельта) на всем интервале анализа называется Прогрессом сходимости цели и отображается на индикаторе сходимости (см. разделы “Таблица целей” и “Цель”).
Внешняя
Внешние течения – это течения, проходящие над моделью или вокруг модели, например, течения вокруг самолетов, автомобилей, зданий и т. д. В задачах с внешними течениями границами дальнего поля являются границы Расчетной области. Рекомендуется использовать Расчетную область по умолчанию, созданную CADFLO. При изменении размера Расчетной области вручную следует иметь в виду, что расположение границ близко к стенкам модели может привести к неверным результатам.
В проектах CADFLO можно одновременно анализировать внешние и внутренние течения, например, обтекание здания потоком воздуха и воздухообмен внутри здания. Если анализ включает как внешние, так и внутренние течения, следует задавать Внешний тип течения.

Угол отклонения потока от расчетного
Этот параметр показывает отклонение потока от расчетного направления. За расчетное принимается направление одной из осей выбранной системы координат. Допустимым считается отклонение потока на угол менее 15°.
Компоненты угла отклонения потока (αi) определяются следующим образом:
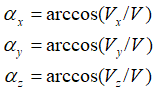
где Vx, Vy, Vz – компоненты скорости потока в направлениях X, Y и Z, а V – абсолютное значение вектора скорости потока.
Несжимаемый
Течения считаются несжимаемыми, если плотность текучей среды зависит только от температуры и концентрации, и эффектами изменения плотности можно пренебречь.
Внутренняя
Внутренними являются течения внутри труб, различных емкостей, систем отопления, вентиляции и кондиционирования воздуха (HVAC) и т.д. Поток поступает в модель и выходит из нее через отверстия, за исключением задач естественной конвекции, когда отверстия могут отсутствовать.
Для расчета внутренней задачи необходимо, чтобы модель была полностью замкнута (см. раздел “Основные принципы”). Чтобы проверить, замкнута ли модель, воспользуйтесь инструментом Проверка геометрии (для получения дополнительной информации обращайтесь к разделу “Проверка геометрии”).
Иррегулярные ячейки
При исследовании расчетной сетки Вы можете заметить наличие Иррегулярных ячеек.
«Иррегулярная» ячейка – это ячейка расчетной сетки, которая находится на границе раздела твердого тела с текучей средой (или на границе раздела твердых тел в случае, когда внутри ячейки оказываются два или более твердых тела). Иррегулярная ячейка частично лежит в одном веществе и частично в другом. Она характеризуется тем, что определить положение границы раздела твердого тела с текучей средой внутри ячейки невозможно. Иррегулярную ячейку не удается разрешить корректно, поэтому она заполняется твердым телом или текучей средой. Приоритетным является заполнение таких ячеек твердым телом для избежания появления "дырок" в текучей среде.
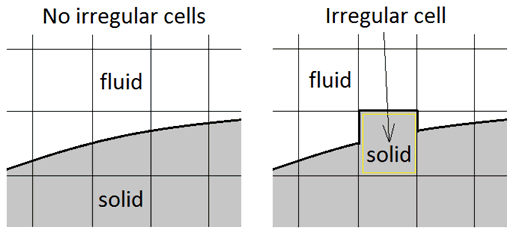
Наличие незначительного количества иррегулярных ячеек в сетке допустимо.
Ошибка локального усечения (LTE)
Ошибка локального усечения (LTE) представляет разницу между точным дифференциальным уравнением и его представлением в виде конечных разностей в точке пространства и времени.
Если y' = f (t, y) – непрерывное дифференциальное уравнение и yn – аппроксимация истинного решения y (tn) на дискретном временном шаге tn, ошибка локального усечения τn на шаге n определяется как τn = y (tn) – yn.
Ошибка локального усечения – это ошибка, создаваемая на одной итерации. Она может использоваться в качестве критерия для выполнения адаптации сетки к решению.
Минимальный зазор
Автоматически определяемый минимальный зазор зависит от размеров модели, расчетной области, а также от размеров поверхностей и тел, на которых заданы источники, начальные и граничные условия. Если в модели есть проточное сечение, размер которого меньше Минимального зазора, то это проточное сечение может оказаться неразрешенным (например, не будет учитываться поток текучей среды через него, или при расчете это сечение будет иметь больший или меньший размер).
Чтобы задать минимальный зазор вручную, нажмите кнопку Задать минимальный зазор  и в поле Минимальный зазор введите нужное значение.
и в поле Минимальный зазор введите нужное значение.
Минимальная толщина стенки
Автоматически определяемая минимальная толщина стенки зависит от размеров модели, расчетной области, а также от заданных объемных и поверхностных источников, начальных условий и поверхностных целей. Минимальная толщина стенки влияет на дробление сетки только на таких геометрических элементах, как острые кромки, небольшие выступы и т.п. Минимальная толщина стенки не влияет на дробление сетки, если это значение больше либо равно Минимальному зазору.
Чтобы задать минимальную толщину стенки вручную, нажмите кнопку Минимальная толщина стенки  и в поле Минимальная толщина стенки введите нужное значение.
и в поле Минимальная толщина стенки введите нужное значение.
Если параметр Минимальная толщина стенки недоступен, выберите значение Показать для параметра Показать/скрыть значение минимальной толщины стенки в разделе Общие опции в диалоговом окне Опции (см. раздел “Опции”).
Количество уровней
Количество уровней – это количество делений, на которые разбивается заданный диапазон параметра. Можно задать до 254 уровней (делений).
Адаптация сетки
«Адаптация сетки» означает дробление ячеек сетки таким образом, что общее количество ячеек увеличивается до тех пор, пока не будет достигнуто заданное разрешение. CADFLO автоматически выполняет адаптацию сетки в процессе расчета, если заданный уровень разрешения больше или равен шести.
Уровень дробления
Каждое Адаптация сетки имеет критерий и соответствующий уровень. Критерий дробления определяет, какие ячейки должны быть разбиты, а уровень дробления – наименьший размер ячеек, которые могут получиться в результате дробления. В результате дробления ячейка разбивается на восемь равных частей тремя взаимно перпендикулярными плоскостями.
Независимо от того, какие особенности модели разрешаются, наименьший размер ячейки всегда определяется относительно размера ячейки Базовой сетки. Так если N = 0...9 – заданный уровень дробления, ячейки расчетной сетки будут дробиться до ячеек, размер которых будет в 2N раз (в каждом направлении Глобальной системы координат или в (2N)3 раз по объему) меньше размера ячеек базовой сетки.
Ошибка RSM
«Ошибка RSM» – является среднеквадратическим показателем усредненной ошибки поверхности и указывает, насколько хорошей является поверхность в глобальном масштабе при адаптации к экспериментам. Несмотря на то, что в зависимости от случая ошибки в 10 % или менее обычно указывают на то, что поверхность отклика имеет хорошую адаптированную форму, т. е. форма является точной, местоположение глобальных минимумов и максимумов будет точным, хотя фактическое значение может и не быть таковым. Подтверждение глобального оптимума в соответствии с рекомендациями относительно поверхности отклика должно быть подтверждено путем решения рекомендованного оптимума.
Ячейки на границе раздела твердого тела с текучей средой
«Ячейка на границе раздела твердого тела с текучей средой» – это общепринятый термин для описания ячейки расчетной сетки, лежащей на границе раздела твердого тела и текучей среды, т. е. частично находящейся в области текучей среды и частично в области твердого тела.
Тонкий канал
В дополнение к модели Двухмасштабные пристеночные функции подход «тонкий канал» используется для описания потока через узкие пазы (включая поток в трубах, поток на плоскости и круговой поток Куэтта) на грубой сетке (число ячеек, проходящих через паз, составляет не более 7). В соответствии с этим подходом сдвиговое напряжение и плотность теплового потока около стенки рассчитываются с помощью аппроксимации на основе экспериментальных данных.
Распространенный подход, используемый для задания сдвигового напряжения и плотности теплового потока около стенки, называется «толстым каналом».
Продувка
Термин «продувка», который используется совместно с понятием итерации, означает единицу измерения, которая характеризует продолжительность расчета. Это период расчета (он может быть измерен в итерациях или в какой-либо другой единице измерения), за который возмущение потока проходит через пространство расчетной области, заполненное текучей средой. Таким образом, N продувок означает период расчета, за который возмущение потока пересекает расчетную область N раз. Количество итераций, соответствующих одной продувке, определяется как функция количества ячеек. Это значение определяется после начала расчета и выводится в окне Текущая информация при мониторинге расчета (см. раздел “Текущая информация”).
Усеченные ячейки
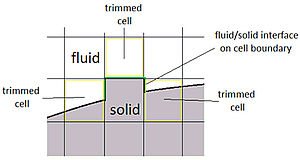
«Усеченная» ячейка – это ячейка расчетной сетки, внутри которой находится по крайней мере один контрольный объем текучей среды и на границу которой приходится по крайней мере одна поверхность раздела твердого тела и текучей среды. Такая ячейка является границей раздела между контрольным объемом текучей среды и контрольным объемом твердого тела в соседней ячейке.
Например:
Ячейки текучей среды, которые являются смежными с иррегулярными ячейками твердого тела, обрезаются |
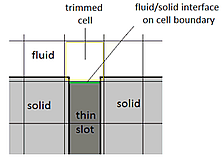
Ячейки текучей среды на конце замкнутой узкой щели |
|
|