Планирование экспериментов

На первом этапе выявляются факторы, влияющие на исследуемое пространство входных параметров, и определяются диапазоны их изменения. Затем выбирается подходящий алгоритм проведения экспериментов для того, чтобы получить как можно больше информации о влиянии выявленных факторов на исследуемый процесс за наименьшее число расчетов.

Традиционные методы Проектирования экспериментов (DoE), которые применяются для моделирования физических экспериментов, как правило, подразумевают исследование границ и в некоторых случаях центра пространства проектных параметров. При расчете выходных параметров могут возникать случайные и систематические ошибки, поэтому для получения статистически достоверных результатов требуется повторять эксперименты несколько раз. Чем больше задано различных входных параметров, т.е. чем больше проводится экспериментов, тем точнее удается выявить влияние факторов на выходные параметры, т.е. тем выше достоверность результатов. Увеличение количества экспериментов позволяет также определить разброс систематических ошибок во всем пространстве входных параметров.

Для компьютерной симуляции необходимо использовать алгоритмы проведения экспериментов с охватом пространства и без стягивания:

• Проектирования с охватом пространства – чтобы исследовать пространство проектирования и получить как можно больше информации, расчетные точки должны быть распределены по исследуемому пространству максимально равномерно, т.е. экспериментальное проектирование "Оптимизация расчета" должно охватывать пространство. При этом предполагается, что информация о функции, на основе которой построена модель симуляции, отсутствует.

• Проектирование без стягивания – обычно заранее неизвестно, какие факторы важны, а какие – нет. Алгоритм проведения экспериментов должен быть таким, чтобы в том случае, если какие-то факторы не оказывают влияния на исследуемый процесс, в результате любого расчета можно было получить информацию о влиянии других факторов на выходные параметры. Т.е. каждый выполненный эксперимент должен позволить получить полезную информацию.

В методе DoE, разработанном и реализованном для CADFLO, используется алгоритм проектирования с охватом пространства Latin Hypercube Design (LHD). Такие процессы проектирования выполняются без стягивания и охватывают все пространство. Для обеспечения охвата пространства проектирования используется минимальное евклидово расстояние между двумя точками. Чем больше это минимальное расстояние, тем лучше экспериментальное проектирование.

Для решения задачи оптимизации применяется метод последовательной оптимизации, предоставленный консалтинговым бюро CQM (SO).

Технология SO объединяет в себе метод построения поверхностей отклика и математическое исследование для систематического и эффективного поиска оптимального варианта. Отношения между проектными параметрами и параметрами отклика описываются моделями поверхностей отклика (Response Surface Models, RSM) (см. раздел “Поверхности отклика”).

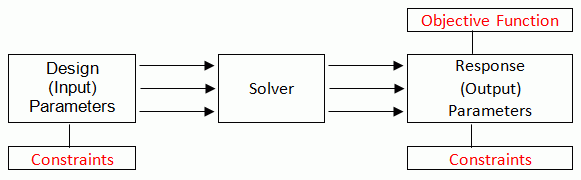
Чтобы найти оптимальный отклик, необходимо задать Целевую функцию с ограничениями или без них (см. раздел “Целевая функция”).